Differentiation

Review basic laws of differentiation

1 The idea of differentiation

• Differentiation is used to analyze the rate at which a function changes with respect to one of its variables at a given point.

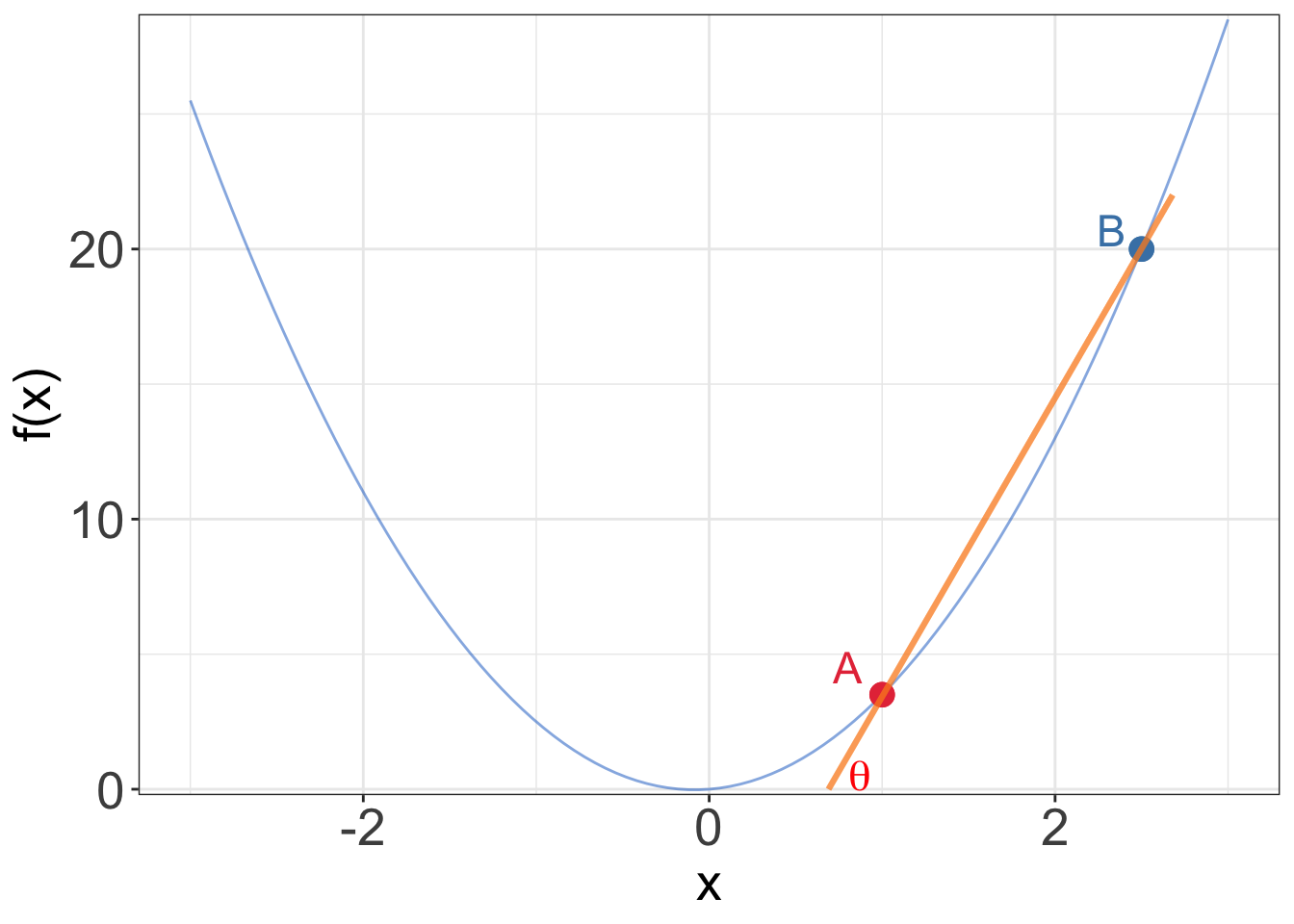
• Let $f(x)$ be a function of $x$ that is represented graphically in Figure 1.

• The line segment connecting the points $A$ and $B$ on the curve is known as the chord (Figure 1a).

• The gradient (i.e., slope) of the chord is defined as the ratio of the change in $y$ to the change in $x$ between points $A$ and $B$ and is equal to $\tan \theta$.

  • ${\displaystyle \text{Gradient of the chord}=\tan \theta =\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=\frac{f(x_B)-f(x_A)}{x_B-x_A}}$.

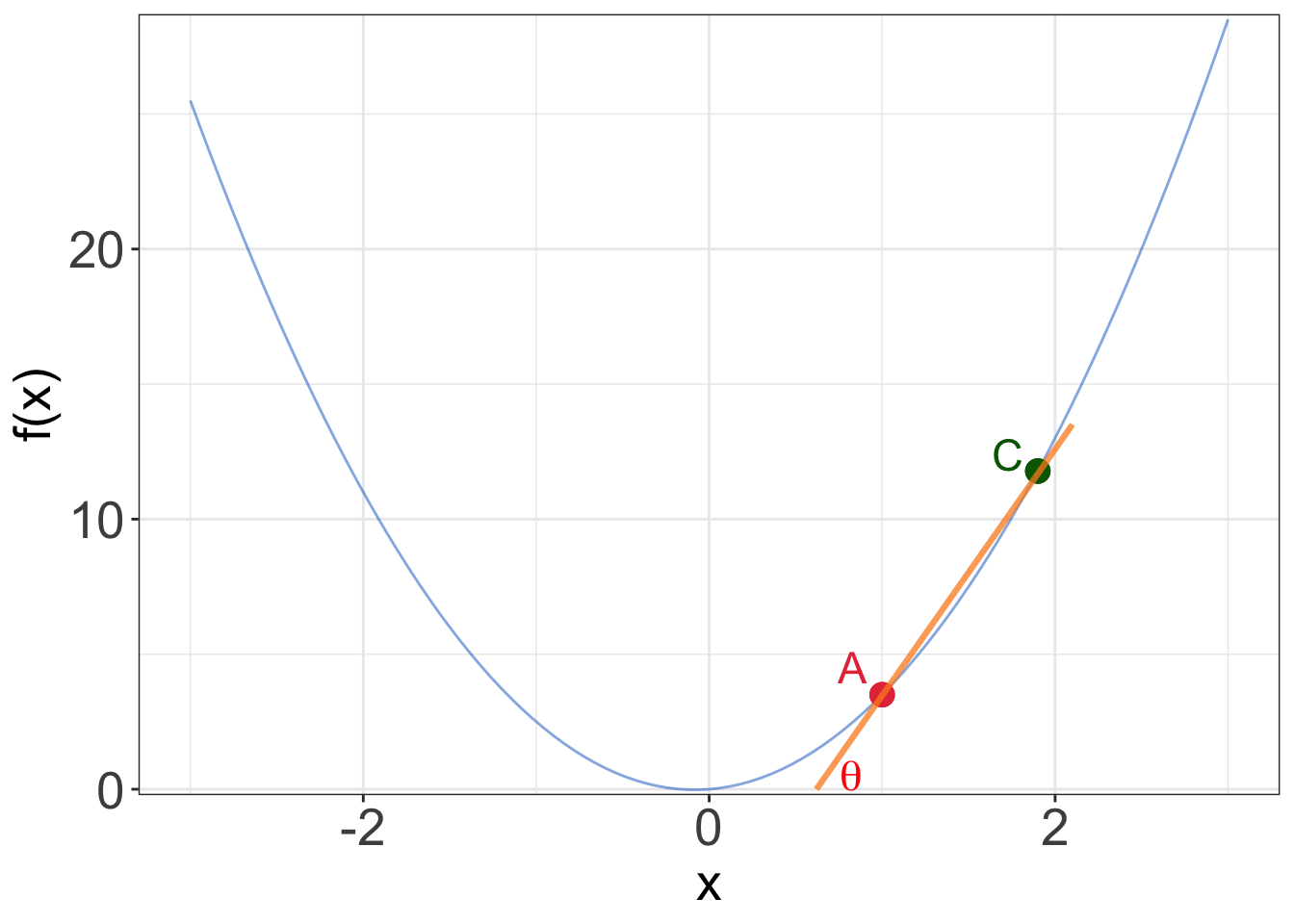
• Assume that the point $B$ moves closer and closer to the point $A$ on the curve ($B$ becomes $C$, Figure 1b)until it coincides with $A$ (Figure 1c).

• In Figure 3c, the chord becomes a line segment that just touches the curve at $A$. This line is referred to as the tangent to the curve at $A$.

(a) Chord between points A and B

(b) Chord between points A and C

(c) Tangent at A

Figure 1: Graph of a function f(x) showing the chord between two points A and B and the tangent at A

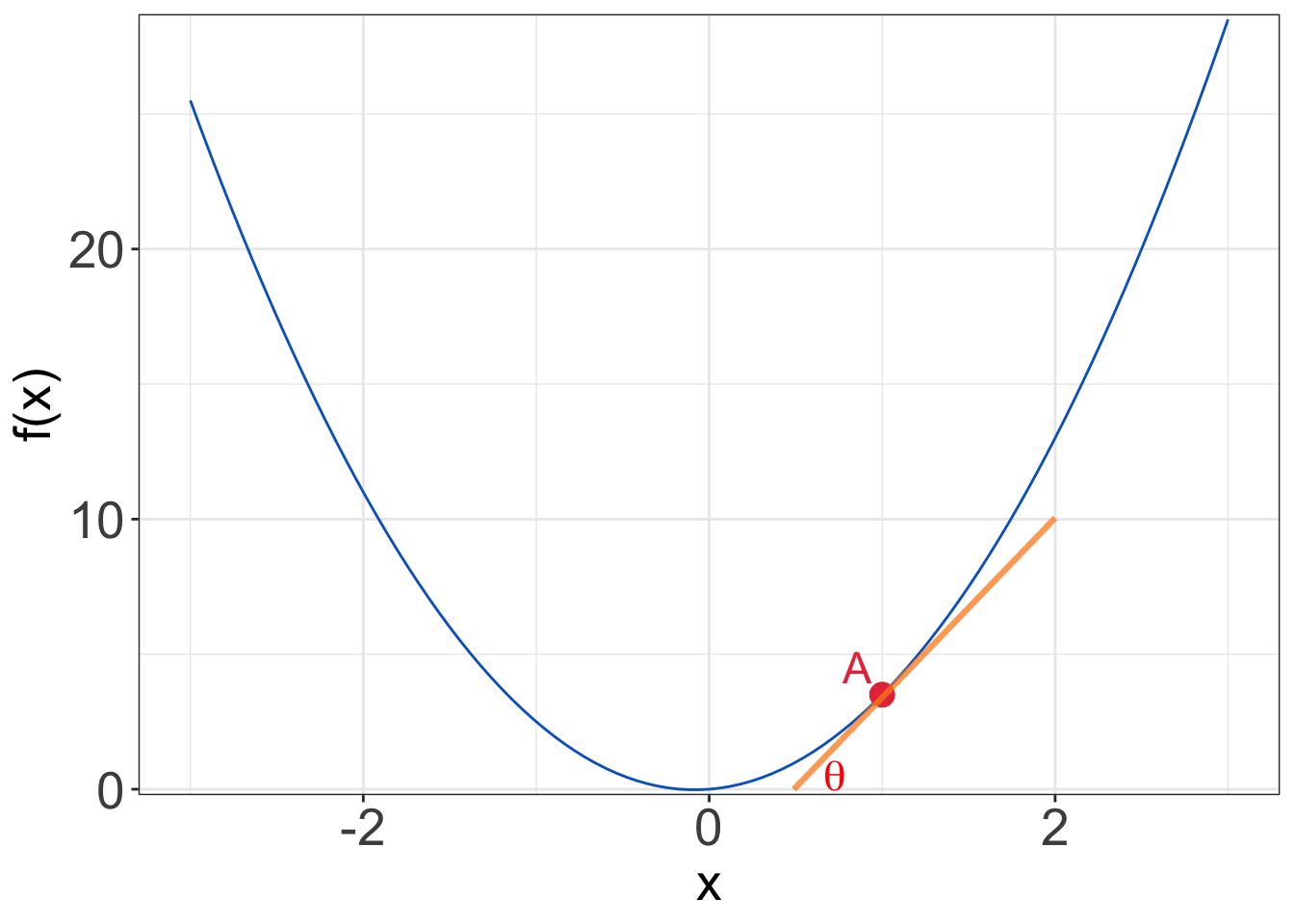
• The gradient of the tangent at $A$ is also known as the instantaneous rate of change of the function $f(x)$ at $A$.

• Let’s now assume two points on the curve, $A=(x,f(x))$ and $B=(x+h,f(x+h))$:

  • From the above discussion, the gradient of the chord connecting $A$ and $B$ is ${\displaystyle \frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=\frac{f(x+h)-f(x)}{(x+h)-x}={\displaystyle \frac{f(x+h)-f(x)}{h}}}$.

  • To find the gradient of the tangent at $A$, we need the point $B$ to become closer and closer to point $A$ (approaches $A$) meaning that $h$ approaches zero.

  • This can be expressed as ${\displaystyle \underset{h\to 0}{lim}\frac{f(x+h)-f(x)}{h}}$.

  • The above limit is referred to as the derivative of the function $f(x)$ with respect to $x$ and is denoted by $f^{\prime }(x)$ or ${\displaystyle \frac{df}{dx}}$.

Example M.10.1

Find the derivative of the function $y=x^3$ with respect to $x$

• Using the definition of the derivative as a limit:

$$y^{\prime }=\frac{dy}{dx}={\displaystyle \underset{h\to 0}{lim}\frac{(x+h{)}^3-x^3}{h}=}$$ $${\displaystyle \underset{h\to 0}{lim}\frac{\cancel{x^3}+3x^{2}h+3x{h}^2+h^3-\cancel{x^3}}{h}=}$$

$${\displaystyle \underset{h\to 0}{lim}\frac{\cancel{h}(3x^2+3xh+h^2)}{\cancel{h}}=}$$

$$3x^2+3x\times 0+0^2=3x^2$$

2 Rules of differentiation

• First principles (i.e., the definition of the derivative as a limit) are rarely used to find the derivative of a function. Instead, there are a set of rules that can be used to find the derivative of different functions:

Table of derivatives of basic functions

Function $y$	Derivative(${\displaystyle \frac{dy}{dx}}$)
Constant $k$	0
$x$	1
$kx$	$k$
$x^n$	$n{x}^{n-1}$
$k{x}^n$	$kn{x}^{n-1}$
$e^x$	$e^x$
$e^{kx}$	$k{e}^{kx}$
$\ln x$	${\displaystyle \frac{1}{x}}$
$\ln kx$	${\displaystyle \frac{1}{x}}$

2.1 Extending the rules of differentiation

2.1.1 Differentiation of a sum or difference of functions

• The derivative of $f(x)\pm g(x)$ is equal to ${\displaystyle \frac{df}{dx}\pm \frac{dg}{dx}}$.

2.1.2 Differentiation of a product of functions

• Let $y=f(x)g(x)$, the derivative is ${\displaystyle \frac{dy}{dx}=f^{\prime }(x)g(x)+f(x)g^{\prime }(x)=\frac{df}{dx}g(x)+f(x)\frac{dg}{dx}}$.

2.1.3 Differentiation of a quotient of functions

• Let $y={\displaystyle \frac{f(x)}{g(x)}}$, the derivative is ${\displaystyle \frac{dy}{dx}={\displaystyle \frac{f^{\prime }(x)g(x)-f(x)g^{\prime }(x)}{(g(x){)}^2}}}$.

Example M.10.2

Find the derivative of the function ${\displaystyle y=2x^3-\frac{1}{\sqrt{x}}+\frac{3}{x^2}}$ with respect to $x$

$$y=2x^3-x^{-\frac{1}{2}}+3x^{-2}\Rightarrow$$ $$y^{\prime }=\frac{dy}{dx}=6x^2+\frac{1}{2}{x}^{-\frac{3}{2}}-6x^{-3}=6x^2+\frac{1}{2\sqrt{x^3}}-\frac{6}{x^3}$$

Example M.10.3

Find the derivative of the function ${\displaystyle y=e^{2x}-e^{-5x}}$ with respect to $x$

$$y^{\prime }=\frac{dy}{dx}=2e^{2x}+5e^{-5x}$$

Example M.10.4

Find the derivative of the function ${\displaystyle y=\frac{e^x}{x^2}}$ with respect to $x$

1. Using the product rule:

$${\displaystyle y=\frac{e^x}{x^2}=x^{-2}{e}^x\Rightarrow }$$

$${\displaystyle \frac{dy}{dx}=-2x^{-3}{e}^x+x^{-2}{e}^x=\frac{e^x}{x^3}(-2+x)=\frac{e^x(x-2)}{x^3}}$$

2. Using the quotient rule:

$${\displaystyle y=\frac{e^x}{x^2}\Rightarrow }$$

$${\displaystyle \frac{dy}{dx}=\frac{e^x{x}^2-e^x(2x)}{(x^2{)}^2}=\frac{e^{x}x(x-2)}{x^4}=\frac{e^x(x-2)}{x^3}}$$

• Both methods yield the same result.

Exercise M.10.1

Find the derivative of the function ${\displaystyle y=\ln (5t)-e^t+\frac{1}{\sqrt[3]{t}}}$ with respect to $t$

$$y=\ln (5t)-e^t+t^{-\frac{1}{3}}\Rightarrow$$ $$y^{\prime }=\frac{dy}{dt}=\frac{1}{t}-e^t-\frac{1}{3}{t}^{-\frac{4}{3}}=\frac{1}{t}-e^t-\frac{1}{3\sqrt[3]{t^4}}$$

3 Chain rule

• This method is used to find the derivative of a composite function (i.e., a function within a function), e.g., $e^{x^3+4x}$ represents the exponential function of a polynomial.

• The composite function is denoted by $y=f(g(x))$. So, in the above example, $f(g)=e^g$ and $g(x)=x^3+4x$.

• Let $y=f(g(x))$, the chain rule states that the derivative is ${\displaystyle \frac{dy}{dx}=\frac{df}{dg}\times \frac{dg}{dx}=f^{\prime }(g(x))\times g^{\prime }(x)}$.

Example M.10.5

Find the derivative of the function $y={\displaystyle e^{x^3+4x}}$ with respect to $x$

$$f(g)=e^g,g(x)=x^3+4x\Rightarrow$$ $$f^{\prime }(g)=e^g,g^{\prime }(x)=3x^2+4\Rightarrow$$ $$\frac{dy}{dx}=e^{x^3+4x}\cdot (3x^2+4)$$

Exercise M.10.2

Find the derivative of the function $y=(2x^2+3x{)}^3$ with respect to $x$

$$f(g)=g^3,g(x)=2x^2+3x\Rightarrow$$

$$f^{\prime }(g)=3g^2,g^{\prime }(x)=4x+3\Rightarrow$$ $$\frac{dy}{dx}=3(2x^2+3x{)}^2\cdot (4x+3)$$

4 Higher derivatives

• The derivative ${\displaystyle \frac{dy}{dx}}$ of the function $y=f(x)$ is referred to as the first derivative.

• If the first derivative is differentiated again, the result is referred to as the second derivative and is denoted by ${\displaystyle \frac{d^{2}y}{d{x}^2}}$ or $f^{″}(x)$.

• Similarly, the third derivative is ${\displaystyle \frac{d^{3}y}{d{x}^3}}$ or $f^{‴}(x)$, and so on.

• The second and the higher derivatives are referred to as higher derivatives.

• Example: Let ${\displaystyle y=x^4+2x^2+6x+7}$:

  • ${\displaystyle \frac{dy}{dx}=y^{\prime }=4x^3+4x+6}$.

  • ${\displaystyle \frac{d^{2}y}{d{x}^2}=y^{″}=12x^2+4}$.

  • ${\displaystyle \frac{d^{3}y}{d{x}^3}=y^{‴}=24x}$.

5 Partial derivatives

• If the function contains more than one variable, the derivative with respect to one variable, keeping the other variables constant, is referred to as a partial derivative.

• Example: Let $z=f(x,y)=x^3+4xy+y^2$:

  • The partial derivative of $z$ with respect to $x$ is ${\displaystyle \frac{\partial z}{\partial x}=3x^2+4y}$ (keeping $y$ constant).

  • The partial derivative of $z$ with respect to $y$ is ${\displaystyle \frac{\partial z}{\partial y}=4x+2y}$ (keeping $x$ constant).

Example M.10.6

Find the derivative of the function $f(x,y)=x^{2}y\ln (x{y}^2)$ with respect to $x$

$$\frac{\partial f}{\partial x}=2xy\ln (x{y}^2)+x^{2}y\times \frac{1}{x}=2xy\ln (x{y}^2)+xy=xy(2\ln (x{y}^2)+1)$$

6 Implicit differentiation

6.1 Difference between explicit and implicit functions

6.1.1 Explicit function

• $y$ is said to be an explicit function of $x$ if variable $y$ is separated on one side of the equation and $x$ is on the other side.

• Example: $y=2x^2+3x+4$.

6.1.2 Implicit function

• $y$ is said to be an implicit function of $x$ if the variables $x$ and $y$ are not separated on either side of the equation (i.e., $x$ and $y$ are mixed).

• Example: $x^2+y^2=25$.

• In the above example, the terms can be rearranged to make $y$ explicit, but in some cases, this rarrangement to separate $x$ and $y$ is not possible.

• In such cases, the derivative of $y$ with respect to $x$ can be found using the implicit differentiation method without the need to obtain $y$ in terms of $x$ explicitly.

6.2 The method of implicit differentiation

• Let $x^3+2y=1+y^2$, implicit differentiation can be used to find ${\displaystyle \frac{dy}{dx}}$ as follows:

  • Differentiate both sides of the equation with respect to $x$:

    • Left side: ${\displaystyle \frac{d}{dx}(x^3+2y)=3x^2+2\frac{dy}{dx}}$.

    • Right side: ${\displaystyle \frac{d}{dx}(1+y^2)=0+2y\frac{dy}{dx}}$.

    • Equate the two sides: ${\displaystyle 3x^2+2\frac{dy}{dx}=2y\frac{dy}{dx}\Rightarrow 3x^2=2y\frac{dy}{dx}-2\frac{dy}{dx}\Rightarrow 3x^2=2\frac{dy}{dx}(y-1)}$.

    • Therefore, ${\displaystyle \frac{dy}{dx}=\frac{3x^2}{2(y-1)}}$.

      Note

      • The derivative of $y^2$ on the right side was found using the chain rule.

      • This is considered as a function of function.

      • $f(y)=y^2\Rightarrow f^{\prime }(y)=2y$ and $y(x)=y\Rightarrow y^{\prime }(x)={\displaystyle \frac{dy}{dx}}$.

      • Using the chain rule: ${\displaystyle \frac{d}{dx}(y^2)=f^{\prime }(y)\cdot y^{\prime }(x)=2y{\displaystyle \frac{dy}{dx}}}$.

Example M.10.7

Find the derivative ${\displaystyle \frac{dy}{dx}}$ of the function $x^4-3xy=6$

1. Rearrange the equation to express $y$ explicitly:

$$x^4-3xy=6\Rightarrow y=\frac{x^4-6}{3x}(\text{apply quotient rule}\Rightarrow )$$

$${\displaystyle \frac{dy}{dx}=\frac{4x^3\times 3x-3(x^4-6)}{(3x{)}^2}=\frac{12x^4-3x^4+18}{9x^2}=\frac{9x^4+18}{9x^2}=x^2+\frac{2}{x^2}}$$

2. Using implicit differentiation:

$${\displaystyle \frac{d}{dx}(x^4-3xy)={\displaystyle \frac{d}{dx}(6)\Rightarrow }}$$

$$4x^3-3y-3x{\displaystyle \frac{dy}{dx}=0\Rightarrow }$$

$$3x{\displaystyle \frac{dy}{dx}=4x^3-3y\Rightarrow }$$

$${\displaystyle \frac{dy}{dx}=\frac{4x^3-3y}{3x}}$$

• If $y$ cannot expressed explicitly in terms of $x$, then ${\displaystyle \frac{dy}{dx}}$ contains both $x$ and $y$ terms.

• However, in this particular example, $y$ can be expressed explicitly in terms of $x$.

• Therefore, we can simplify the derivative ${\displaystyle \frac{dy}{dx}}$ by substituting $y={\displaystyle \frac{x^4-6}{3x}}$ into the equation.

$${\displaystyle \frac{dy}{dx}=\frac{4x^3-3y}{3x}=\frac{4x^3-3\left(\frac{x^4-6}{3x}\right)}{3x}=x^2+\frac{2}{x^2}}$$

• Both methods yield the same result.

7 References

• Differentiation. Help Engineers Learn Mathematics (HELM) workbooks. Loughborough University. Retrieved September 03, 2024, from https://www.lboro.ac.uk/media/media/schoolanddepartments/mlsc/downloads/HELM%20Workbook%2011%20Differentiation.pdf

• Derivatives. In Calculus: Volume 1 (OpenStax). Retrieved September 03, 2024, from https://openstax.org/books/calculus-volume-1/pages/3-introduction

8 Add your comments